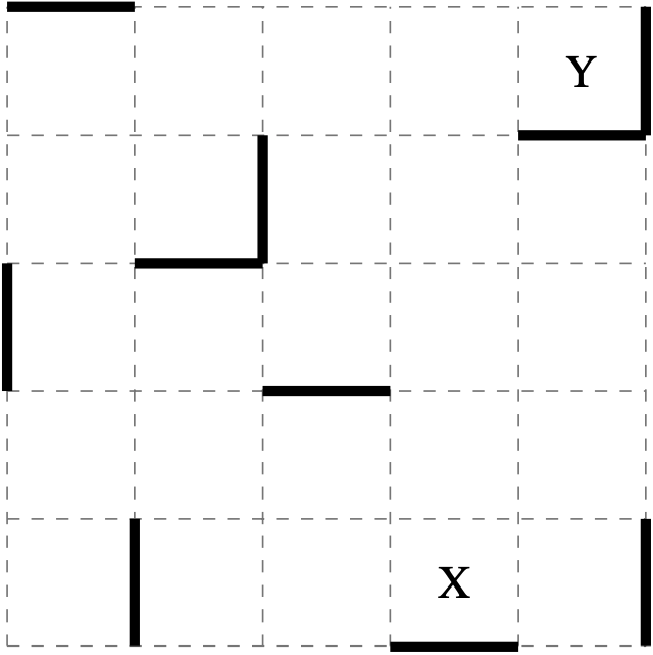
Astrid the astronaut is floating in a grid. Each time she pushes off she keeps gliding until she collides with a solid wall, marked by a thicker line.

From such a wall she can propel herself either parallel or perpendicular to the wall, but always travelling directly \(\leftarrow, \rightarrow, \uparrow, \downarrow\). Floating out of the grid means death.

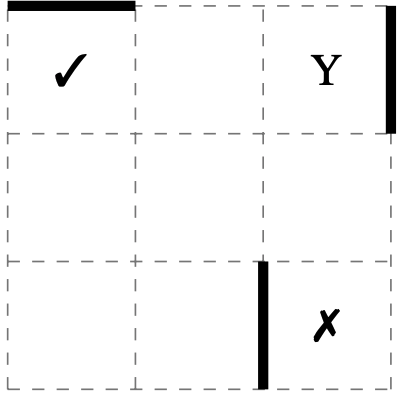
In grid below, Astrid can reach square Y from square ✔. But if she starts from square ✘ there is no wall to stop her and she will float past Y and out of the grid.

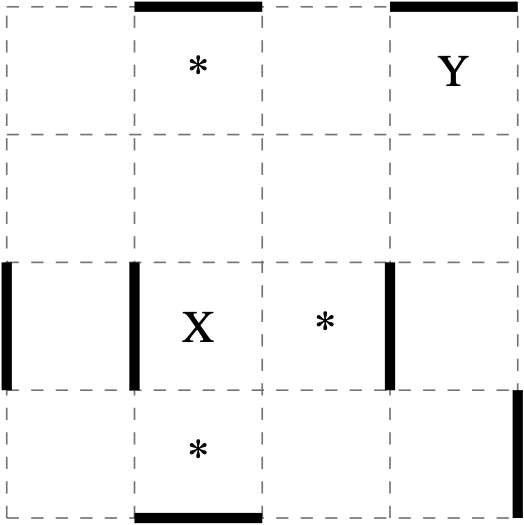
In following grid, from square \(\text{X}\) Astrid can float to three different squares with one push (each is marked with *).

Push \(\leftarrow\) is not possible from \(\text{X}\) due to the solid wall to the left.

From \(\text{X}\) it takes three pushes to stop safely at square \(\text{Y}\), namely \(\downarrow, \rightarrow, \uparrow\).

The sequence \(\uparrow, \rightarrow\) would have Astrid float past \(\text{Y}\) and out of the grid.

In the grid below, what is the least number of pushes that Astrid can make to safely travel from \(\text{X}\) to \(\text{Y}\)?